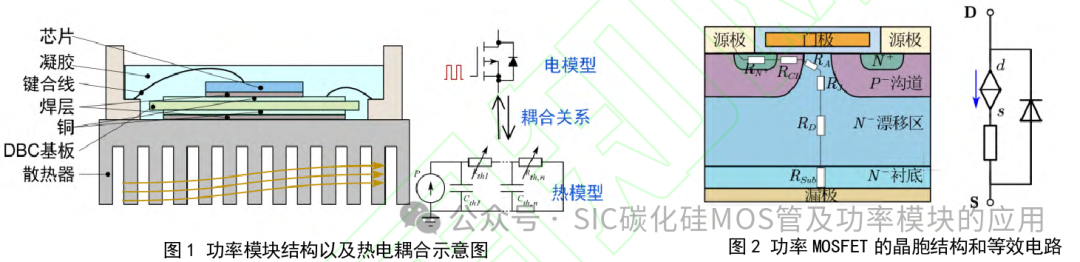
 如图1所示,功率芯片必须以分立器件或功率模块的形式进行封装。功率封装是半导体芯片和其他封装结构的组合,可以提供辅助电气、热和机械的功能[ 13– 15] 。由于功率芯片会散发大量热量,封装及散热系统对芯片结温的影响较大。为分析安全边界,主需要研究三个问题:(1) Si C MOSFET 的热电耦合模型;(2) 封装和散热系统的热分析; (3) 电气和热学参数的耦合机制。 在此前的研究中,很少有文章关注近限边界下的电气和散热评估,缺乏高温稳定性的机理分析。文献[16– 18] 对SiC MOSFET的电热模型进行了大量研究。但这些模型都没有针对热测试环境进行优化,比较复杂难以在系统仿真中实用。对于功率模块,制造商通常只在数据手册中提供结壳热阻。实际上,散热系统的热阻也很关键,特别是在高温应用中,温度变化得非常快,一些相关的电气参数也变得极为敏感[ 19–22] 。然而,尽管有很多关于外部散热系统特性的研究[ 23-24] ,但很少有研究关注散热系统与器件电热模型的协同求解。热学参数与电学参数的耦合机制是探寻功率模块高温工作能力的关键,电气产生的损耗会影响热分布,进而结温也会决定器件的电气特性,较低结温下这种耦合可近 似为负反馈中的小波动,近限状态下它向正反馈的迅速过度是引起热失控的主要原因。 本文提出一种评估SiC功率模块在高温下应用能力的方法,来探索安全应用边界。本文分为三个部分:第二节建立了SiC MOSFET热电模型,第三节对功率模块的散热系统进行热分析,第四节为高温下模块的稳定性分析。 1 SiC MOSFET温度相关的器件模型 文选择了Wolfspeed公司第二代SiC MOSFET功率芯片CPM212000025B作为研究对象,该功率器件为垂直器件, 其晶胞单元结构及等效电路如图2所示。垂直器件与普通横向器件的主要区别在于,垂直器件具有较大的N-漂移区,表现为电阻的特征。因此,功率器件可以被建模为普通横向MOSFET与剩余电阻Rs。 1.1 受温度影响较大的半导体材料参数 决定SiC器件温度依赖性的关键参数是体电子迁移率µn,bulk,它与温度的关系可以由等式(1)给出[ 25] 。
如图1所示,功率芯片必须以分立器件或功率模块的形式进行封装。功率封装是半导体芯片和其他封装结构的组合,可以提供辅助电气、热和机械的功能[ 13– 15] 。由于功率芯片会散发大量热量,封装及散热系统对芯片结温的影响较大。为分析安全边界,主需要研究三个问题:(1) Si C MOSFET 的热电耦合模型;(2) 封装和散热系统的热分析; (3) 电气和热学参数的耦合机制。 在此前的研究中,很少有文章关注近限边界下的电气和散热评估,缺乏高温稳定性的机理分析。文献[16– 18] 对SiC MOSFET的电热模型进行了大量研究。但这些模型都没有针对热测试环境进行优化,比较复杂难以在系统仿真中实用。对于功率模块,制造商通常只在数据手册中提供结壳热阻。实际上,散热系统的热阻也很关键,特别是在高温应用中,温度变化得非常快,一些相关的电气参数也变得极为敏感[ 19–22] 。然而,尽管有很多关于外部散热系统特性的研究[ 23-24] ,但很少有研究关注散热系统与器件电热模型的协同求解。热学参数与电学参数的耦合机制是探寻功率模块高温工作能力的关键,电气产生的损耗会影响热分布,进而结温也会决定器件的电气特性,较低结温下这种耦合可近 似为负反馈中的小波动,近限状态下它向正反馈的迅速过度是引起热失控的主要原因。 本文提出一种评估SiC功率模块在高温下应用能力的方法,来探索安全应用边界。本文分为三个部分:第二节建立了SiC MOSFET热电模型,第三节对功率模块的散热系统进行热分析,第四节为高温下模块的稳定性分析。 1 SiC MOSFET温度相关的器件模型 文选择了Wolfspeed公司第二代SiC MOSFET功率芯片CPM212000025B作为研究对象,该功率器件为垂直器件, 其晶胞单元结构及等效电路如图2所示。垂直器件与普通横向器件的主要区别在于,垂直器件具有较大的N-漂移区,表现为电阻的特征。因此,功率器件可以被建模为普通横向MOSFET与剩余电阻Rs。 1.1 受温度影响较大的半导体材料参数 决定SiC器件温度依赖性的关键参数是体电子迁移率µn,bulk,它与温度的关系可以由等式(1)给出[ 25] 。 其中Tj是结温。然而,由于 SiO2/SiC 界面处的界面陷阱密度大,沟道的电子效应迁移率要比体电子迁移率小得多。因此它也依赖于Vgs的大小,同时呈现出正温度系数[ 26] 。沟道电子的场效应迁移率与温度之间的近似关系为:
其中Tj是结温。然而,由于 SiO2/SiC 界面处的界面陷阱密度大,沟道的电子效应迁移率要比体电子迁移率小得多。因此它也依赖于Vgs的大小,同时呈现出正温度系数[ 26] 。沟道电子的场效应迁移率与温度之间的近似关系为: 其中β是正值。这个方程是一个简化方程,主要说明界面陷阱处的库仑散射在影响沟道迁移率的因素中起主导作用[ 27] 。另一个受温度影响的参数是带隙Eg,它与温度的关系可以用等式(3)表示[ 28]:
其中β是正值。这个方程是一个简化方程,主要说明界面陷阱处的库仑散射在影响沟道迁移率的因素中起主导作用[ 27] 。另一个受温度影响的参数是带隙Eg,它与温度的关系可以用等式(3)表示[ 28]: 1.2 阈值电压 阈值电压是 MOSFET 器件的一个关键热敏感参数。通常它可以通过方程(5)给出的线性拟合方程来建模。
1.2 阈值电压 阈值电压是 MOSFET 器件的一个关键热敏感参数。通常它可以通过方程(5)给出的线性拟合方程来建模。 其中Vth300是常温300K时的阈值电压,kvth是阈值电压的温度系数。对于所研究的芯片,实验提取的Vth300为2.78V, kvth为6.31mV。 1.3 导通电阻 功率MOSFET器件的导通电阻Ron是指漏源电流Ids流过的所有区域的电阻之和。Ron的大小决定了器件的通态损耗, 并可能影响MOSFET导通电流的能力。在图2中,SiC MOSFET的导通电阻由6个部分组成,RN+是源极扩散电阻,RCH是沟道电阻,RA是累积电阻,RJ是两个体区之间区域的JFET元件电阻,RD是漂移区域电阻,RSub为衬底电阻。高压功率 MOSFET导通电阻的主要部分是沟道电阻、JFET电阻和漂移区电阻[ 25] 。在本文中,总漏源电阻由沟道电阻Rch和残余电阻Rs表示,其中Rs主要包括漂移电阻和JFET电阻。 图 2.5中d和s之间的部分由以下两个方程建模:
其中Vth300是常温300K时的阈值电压,kvth是阈值电压的温度系数。对于所研究的芯片,实验提取的Vth300为2.78V, kvth为6.31mV。 1.3 导通电阻 功率MOSFET器件的导通电阻Ron是指漏源电流Ids流过的所有区域的电阻之和。Ron的大小决定了器件的通态损耗, 并可能影响MOSFET导通电流的能力。在图2中,SiC MOSFET的导通电阻由6个部分组成,RN+是源极扩散电阻,RCH是沟道电阻,RA是累积电阻,RJ是两个体区之间区域的JFET元件电阻,RD是漂移区域电阻,RSub为衬底电阻。高压功率 MOSFET导通电阻的主要部分是沟道电阻、JFET电阻和漂移区电阻[ 25] 。在本文中,总漏源电阻由沟道电阻Rch和残余电阻Rs表示,其中Rs主要包括漂移电阻和JFET电阻。 图 2.5中d和s之间的部分由以下两个方程建模: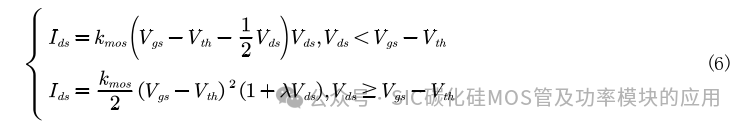 其中Ids是流过节点d和s的电流,Vds是两个节点之间的电压,Vgs是栅极偏置电压,Vth是阈值电压,λ是沟道长度调制。此外,kmos = µnch−fe Cox W/L是与制造相关的参数,其中W为沟道宽度,L为沟道长度,Cox为栅氧化层电容。k和Vth都与温度相关。当器件完全导通时,Vds非常小,因此Rch可以写为:
其中Ids是流过节点d和s的电流,Vds是两个节点之间的电压,Vgs是栅极偏置电压,Vth是阈值电压,λ是沟道长度调制。此外,kmos = µnch−fe Cox W/L是与制造相关的参数,其中W为沟道宽度,L为沟道长度,Cox为栅氧化层电容。k和Vth都与温度相关。当器件完全导通时,Vds非常小,因此Rch可以写为:  其中krs是一个常数系数,α应该接近公式(1)中的2.7。
其中krs是一个常数系数,α应该接近公式(1)中的2.7。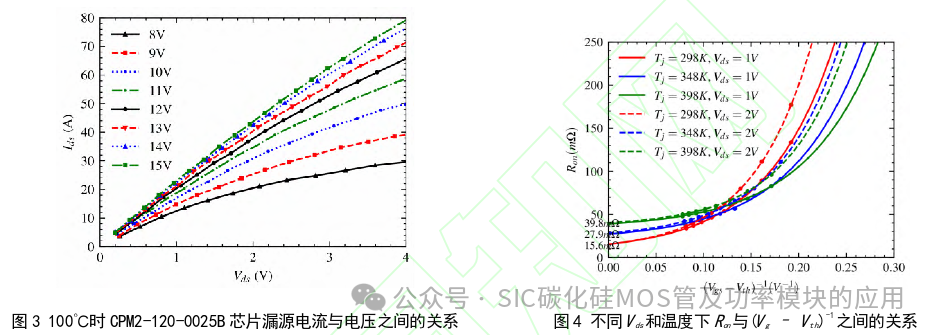 1.4 实验与参数提取 本文通过实验测量了研究对象在不同栅极电压和温度下流过SiC芯片的电流。图3为100℃时漏源电流与电压的 关系,其他温度下关系趋势与之类似。 因为总的导通电阻Ron可以写为:
1.4 实验与参数提取 本文通过实验测量了研究对象在不同栅极电压和温度下流过SiC芯片的电流。图3为100℃时漏源电流与电压的 关系,其他温度下关系趋势与之类似。 因为总的导通电阻Ron可以写为: 公式的第一部分是沟道电阻Rch,Rs为残余电阻。当(Vg–Vth)-1 接近0时,Ron约等于Rs,图4为将特性曲线转化之后的结果,其横轴变量是(Vg–Vth)- 1 ,纵轴变量为Ron。 从总通态电阻Ron中提取Rs,Rs和Rch,它们随温度变化的趋势如图5所示。可以看出,当温度升高时,Rs将越来越占主导地位。与等式(9)预测的趋势一致,Rs随温度呈指数增长,提取的α为3.24,krs为15.6 mΩ。与公式(1)中的 系数值2.7略有不同,可以解释为Rs计算误差以及其他部分电阻如JFET电阻、衬底电阻等的影响。
公式的第一部分是沟道电阻Rch,Rs为残余电阻。当(Vg–Vth)-1 接近0时,Ron约等于Rs,图4为将特性曲线转化之后的结果,其横轴变量是(Vg–Vth)- 1 ,纵轴变量为Ron。 从总通态电阻Ron中提取Rs,Rs和Rch,它们随温度变化的趋势如图5所示。可以看出,当温度升高时,Rs将越来越占主导地位。与等式(9)预测的趋势一致,Rs随温度呈指数增长,提取的α为3.24,krs为15.6 mΩ。与公式(1)中的 系数值2.7略有不同,可以解释为Rs计算误差以及其他部分电阻如JFET电阻、衬底电阻等的影响。 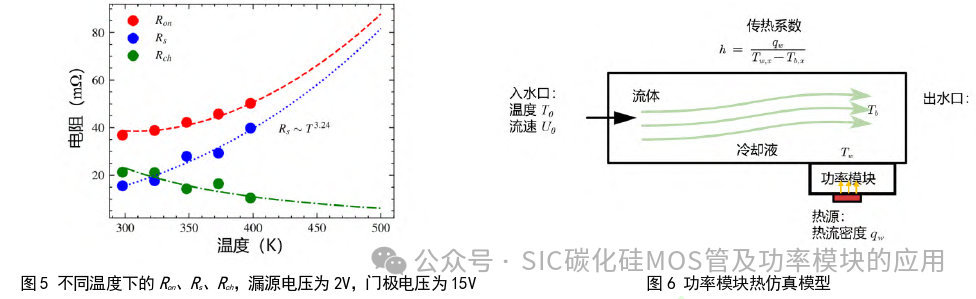 与Rs不同,沟道电阻Rch与温度呈负相关性,提取的krch为0.281 Ω·V,β为 2.4。沟道电阻会稍微减缓功率损 耗的增加速度,但当温度升高时它的减缓效果降低。也就是说,在高温下,温度与发热功率的正反馈会越来越严重, 使得芯片更容易损坏。 2 功率模块和散热系统的热分析 功率模块散热主要有两种方式:传导和对流,而辐射传热不明显。热传导主要发生在功率模块封装的不同层之间。 而热对流主要发生在液冷或风冷散热系统的液固/气固界面。一般在基于产品手册的热评估中,只使用简单的热阻结- 壳热阻Rth,jc或结-空气热阻Rth,ja,但较高温度下的非线性因素会影响温度分布和散热性能,需要详细计算。 2.1 与温度无关的非线性参数
与Rs不同,沟道电阻Rch与温度呈负相关性,提取的krch为0.281 Ω·V,β为 2.4。沟道电阻会稍微减缓功率损 耗的增加速度,但当温度升高时它的减缓效果降低。也就是说,在高温下,温度与发热功率的正反馈会越来越严重, 使得芯片更容易损坏。 2 功率模块和散热系统的热分析 功率模块散热主要有两种方式:传导和对流,而辐射传热不明显。热传导主要发生在功率模块封装的不同层之间。 而热对流主要发生在液冷或风冷散热系统的液固/气固界面。一般在基于产品手册的热评估中,只使用简单的热阻结- 壳热阻Rth,jc或结-空气热阻Rth,ja,但较高温度下的非线性因素会影响温度分布和散热性能,需要详细计算。 2.1 与温度无关的非线性参数 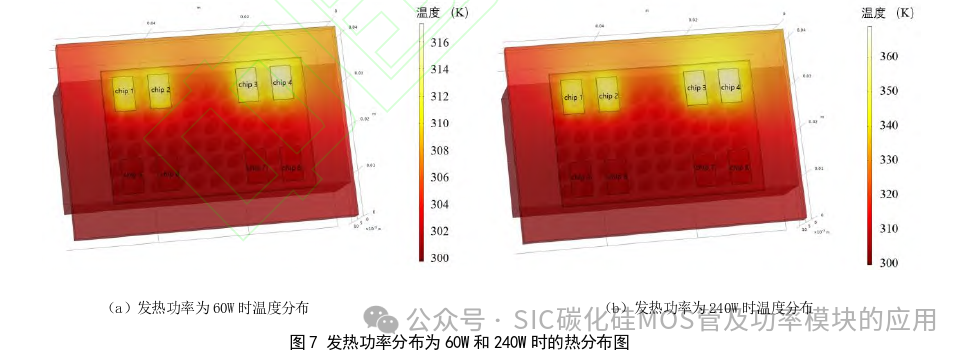 非线性主要可以由三个部分引入:热扩散过程、热对流过程和材料特性的温度依赖性[29]。热扩散效应的含义是 在芯片发热功率越大时,功率芯片与冷却液之间的温差也越大,因此散热面积也越大,从而使得热对流更加有效,即 热扩散效应带来的非线性。对于热对流过程,非线性由冷却液流动条件引入。但在电动汽车等一些应用中,依然可以 认为是线性的,因为它总是处于层流状态或层流和湍流之间过渡的早期阶段。然而,在一些功率非常大的应用中,需要采用相变散热等高效散热方式,非线性会较为明显。在这些情况下,可以使用变化的热阻或热网络模型。 为了研究这个问题,本文建立了如图6所示的仿真模型,仿真在COMSOL软件中进行。选择流体作为传热介质以反 映热对流过程,而通过改变热源功率值来体现热扩散效应。在没有对材料施加温度依赖性的情况下,结果如图 7 所示。计算得到的稳态结-冷却液热阻如表1。随着热功率从60 W增加到240 W,可以看出由于热扩散导致热阻下降非常小, 可以忽略不计。因此,在不考虑温度依赖性的情况下,可以认为传热系数与发热功率值无关。
非线性主要可以由三个部分引入:热扩散过程、热对流过程和材料特性的温度依赖性[29]。热扩散效应的含义是 在芯片发热功率越大时,功率芯片与冷却液之间的温差也越大,因此散热面积也越大,从而使得热对流更加有效,即 热扩散效应带来的非线性。对于热对流过程,非线性由冷却液流动条件引入。但在电动汽车等一些应用中,依然可以 认为是线性的,因为它总是处于层流状态或层流和湍流之间过渡的早期阶段。然而,在一些功率非常大的应用中,需要采用相变散热等高效散热方式,非线性会较为明显。在这些情况下,可以使用变化的热阻或热网络模型。 为了研究这个问题,本文建立了如图6所示的仿真模型,仿真在COMSOL软件中进行。选择流体作为传热介质以反 映热对流过程,而通过改变热源功率值来体现热扩散效应。在没有对材料施加温度依赖性的情况下,结果如图 7 所示。计算得到的稳态结-冷却液热阻如表1。随着热功率从60 W增加到240 W,可以看出由于热扩散导致热阻下降非常小, 可以忽略不计。因此,在不考虑温度依赖性的情况下,可以认为传热系数与发热功率值无关。 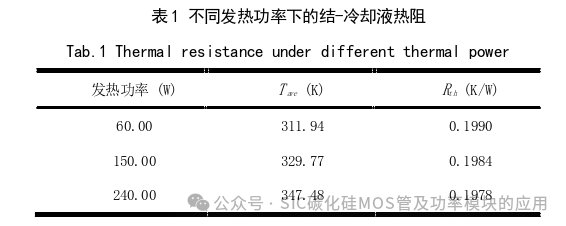 2.2 温度对热阻的影响 与上面讨论的其他两个因素相比,材料的温度依赖性对热阻的影响更大。热传导遵循傅立叶定律,热流密度q等于热导率λ和负温度梯度的乘积,即:
2.2 温度对热阻的影响 与上面讨论的其他两个因素相比,材料的温度依赖性对热阻的影响更大。热传导遵循傅立叶定律,热流密度q等于热导率λ和负温度梯度的乘积,即:  其中关键参数是λ,它是温度的函数,会引入非线性。模块中常用的材料热导率随温度的变化如图8所示[ 29–31] 。
其中关键参数是λ,它是温度的函数,会引入非线性。模块中常用的材料热导率随温度的变化如图8所示[ 29–31] 。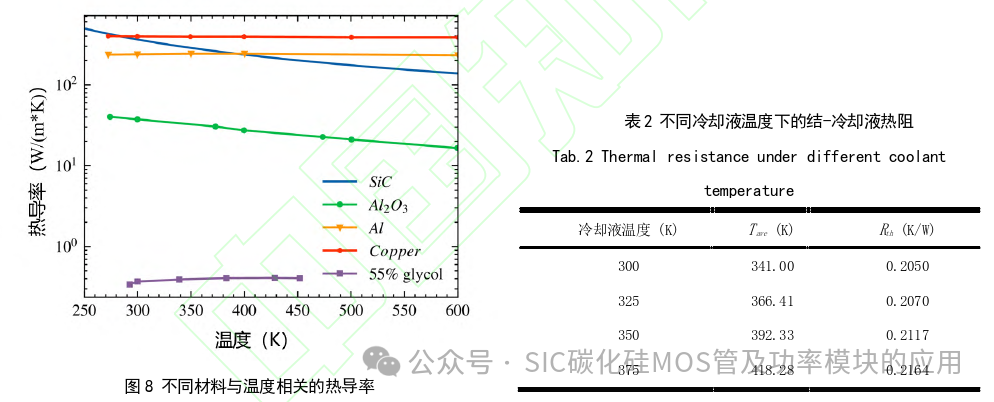 热对流的过程比热传导更复杂,因为它与液体流动密切相关。除了偏微分热方程外,由努塞尔数描述的经验公式通常被用于计算传热系数[ 32] 。
热对流的过程比热传导更复杂,因为它与液体流动密切相关。除了偏微分热方程外,由努塞尔数描述的经验公式通常被用于计算传热系数[ 32] 。 其中h是对流传热系数,λ是流体的热导率,L是特征长度,Nu是努塞尔数。λ、Nu 都是温度的函数。 表2为不同液体温度下的结-冷却液热阻的计算结果,图9为仿真的温度分布图。可以发现,当液体温度从300K 增加到375K时,结与液体之间的热阻变化约为0.01 K/W。在1kW 的功率损耗下,结温误差可以估计为10K。当 液体温度变化很大时,温度依赖性不能忽略,例如电动汽车冷却液。
其中h是对流传热系数,λ是流体的热导率,L是特征长度,Nu是努塞尔数。λ、Nu 都是温度的函数。 表2为不同液体温度下的结-冷却液热阻的计算结果,图9为仿真的温度分布图。可以发现,当液体温度从300K 增加到375K时,结与液体之间的热阻变化约为0.01 K/W。在1kW 的功率损耗下,结温误差可以估计为10K。当 液体温度变化很大时,温度依赖性不能忽略,例如电动汽车冷却液。 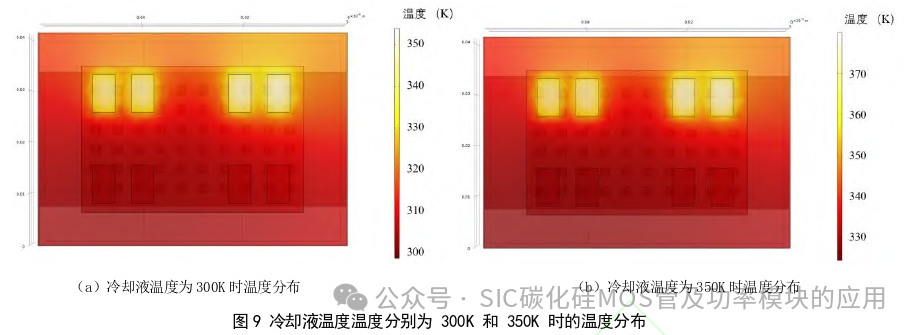 2.3 温度相关的热阻模型 如上所述,热阻几乎与功率损耗无关,但对温度比较敏感。虽然散热功率的大小不会明显改变热阻,但它会影响 功率模块和散热系统内部的温度分布,然后使总热阻发生变化。由于温度分布计算需要较长的时间,而模块中间层的 温度并不需要特别关注,因此可以将结到参考点的热阻Rth,jr用二次函数拟合。
2.3 温度相关的热阻模型 如上所述,热阻几乎与功率损耗无关,但对温度比较敏感。虽然散热功率的大小不会明显改变热阻,但它会影响 功率模块和散热系统内部的温度分布,然后使总热阻发生变化。由于温度分布计算需要较长的时间,而模块中间层的 温度并不需要特别关注,因此可以将结到参考点的热阻Rth,jr用二次函数拟合。 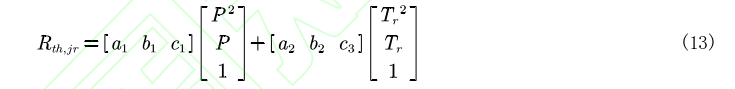 其中P是从器件的发热功率,Tr是参考点的温度,P和Tr可以被认为是相互独立的。 3 稳态温度稳定性评估 在常温或高温条件下的应用中,器件的功率损耗与结温之间始终存在正反馈。温度升高,功率损耗就会增加,而增加的功率损耗又会反过来是结温升高。很明显,当导通电流或结温升高到一定程度时,结温将对导通电流或功率损耗的增加极为敏感。如果温度或电流继续增加,就会发生热失控。 3.1 热失控机理 SiC MOSFET自发热产生的热量可以用等式(14)表示:
其中P是从器件的发热功率,Tr是参考点的温度,P和Tr可以被认为是相互独立的。 3 稳态温度稳定性评估 在常温或高温条件下的应用中,器件的功率损耗与结温之间始终存在正反馈。温度升高,功率损耗就会增加,而增加的功率损耗又会反过来是结温升高。很明显,当导通电流或结温升高到一定程度时,结温将对导通电流或功率损耗的增加极为敏感。如果温度或电流继续增加,就会发生热失控。 3.1 热失控机理 SiC MOSFET自发热产生的热量可以用等式(14)表示: 另外,热阻也可以简单地表示为散热功率与温度差的关系,即
另外,热阻也可以简单地表示为散热功率与温度差的关系,即  其中Pdiss是发热功率,Ta是环境温度,Rthja是结和环境之间的热阻。在这种情况下,Rthja是一个独立于Tj 和Id的常数值。
其中Pdiss是发热功率,Ta是环境温度,Rthja是结和环境之间的热阻。在这种情况下,Rthja是一个独立于Tj 和Id的常数值。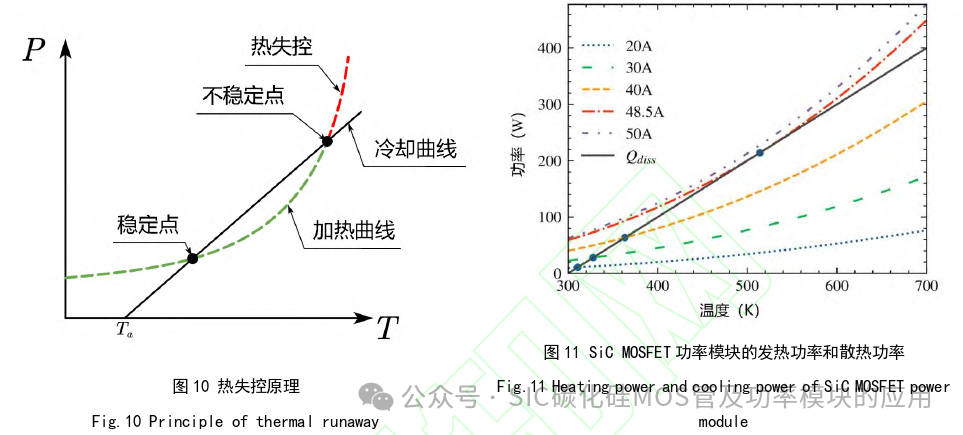 图10为热失控的原理。当Pcond > Pdiss时,发热功率大于散热功率,结温将升高到新的平衡点或发生热失控。当Pcond < Pdiss 时,散热功率大于发热功率,结温将降到较低的热平衡点。当处于稳定点时, Pcond = Pdiss, 系统达到热平衡,负反馈可以拉回 小的偏移量。但是如果在不稳定点实现热平衡,一个小的扰动就可以使系统很快达到热失控。 图11为不同工作电流下的导通损耗功率和散热功率的仿真结果。在该仿真中,温度为300 K时的导通电阻被设置为25 mΩ, 等式 (16) 中的系数为 2.4,结与环境之间的热阻为1 K/W。虚线为在不同导通电流下功率器件的发热功率与结温的关系, 实线为散热系统的散热功率与结温的关系。 很明显,实线(散热功率)和虚线(发热功率)之间会有两个交点,只有在第一个交叉点处才能达到热平衡。通过标记所 有第一个交点,可以获得在不同导通电流下的稳态工作点。同时当线性散热功率曲线与指数发热功率线相切时,可以算出最大工作条件为导通电流为48.5A,结温为514K(241 ℃)。
图10为热失控的原理。当Pcond > Pdiss时,发热功率大于散热功率,结温将升高到新的平衡点或发生热失控。当Pcond < Pdiss 时,散热功率大于发热功率,结温将降到较低的热平衡点。当处于稳定点时, Pcond = Pdiss, 系统达到热平衡,负反馈可以拉回 小的偏移量。但是如果在不稳定点实现热平衡,一个小的扰动就可以使系统很快达到热失控。 图11为不同工作电流下的导通损耗功率和散热功率的仿真结果。在该仿真中,温度为300 K时的导通电阻被设置为25 mΩ, 等式 (16) 中的系数为 2.4,结与环境之间的热阻为1 K/W。虚线为在不同导通电流下功率器件的发热功率与结温的关系, 实线为散热系统的散热功率与结温的关系。 很明显,实线(散热功率)和虚线(发热功率)之间会有两个交点,只有在第一个交叉点处才能达到热平衡。通过标记所 有第一个交点,可以获得在不同导通电流下的稳态工作点。同时当线性散热功率曲线与指数发热功率线相切时,可以算出最大工作条件为导通电流为48.5A,结温为514K(241 ℃)。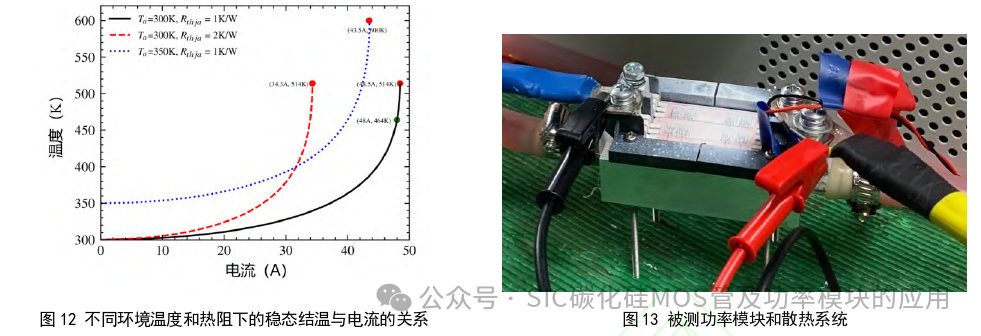 用以下两个方程可以解析地求出模块地最大工作点:
用以下两个方程可以解析地求出模块地最大工作点: 其中第一个方程表示热平衡,第二个方程表示最大工作点。将式(14)和(17)代入式(18),可以推导出该仿真情况下的 热失控条件。
其中第一个方程表示热平衡,第二个方程表示最大工作点。将式(14)和(17)代入式(18),可以推导出该仿真情况下的 热失控条件。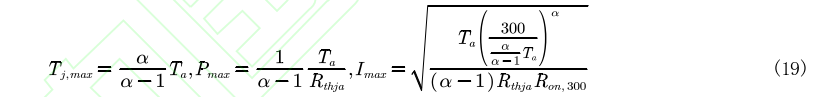 图12描绘了不同环境温度和热阻下的热失控过程。随着电流的增加,结温以加速的方式增加。可以发现,接近最大值的工作点是极其“不稳定”的,此时0.5 A的电流差可以在300 K的环境温度和1K/W的热阻下引起50°C的结 温差。因此,在实际应用中必须留下较大的安全裕度。热阻和环境温度对模块能导通的最大电流影响较大,为了充分利用SiC器件的优秀性能,应仔细设计散热系统以避免热失控。 3.2 搭建实验平台 本文搭建了一个测试平台来验证所提出的模型并评估高温稳定性。如图 13 所示,功率模块封装被打开,SiC裸片表面经过喷漆处理,可通过红外热成像仪获取准确温度。测试装置的参数列于表3,其中直流电流源用于加热功率模块,红外热像仪测量稳态结温,恒温冷却循环器用于散热。
图12描绘了不同环境温度和热阻下的热失控过程。随着电流的增加,结温以加速的方式增加。可以发现,接近最大值的工作点是极其“不稳定”的,此时0.5 A的电流差可以在300 K的环境温度和1K/W的热阻下引起50°C的结 温差。因此,在实际应用中必须留下较大的安全裕度。热阻和环境温度对模块能导通的最大电流影响较大,为了充分利用SiC器件的优秀性能,应仔细设计散热系统以避免热失控。 3.2 搭建实验平台 本文搭建了一个测试平台来验证所提出的模型并评估高温稳定性。如图 13 所示,功率模块封装被打开,SiC裸片表面经过喷漆处理,可通过红外热成像仪获取准确温度。测试装置的参数列于表3,其中直流电流源用于加热功率模块,红外热像仪测量稳态结温,恒温冷却循环器用于散热。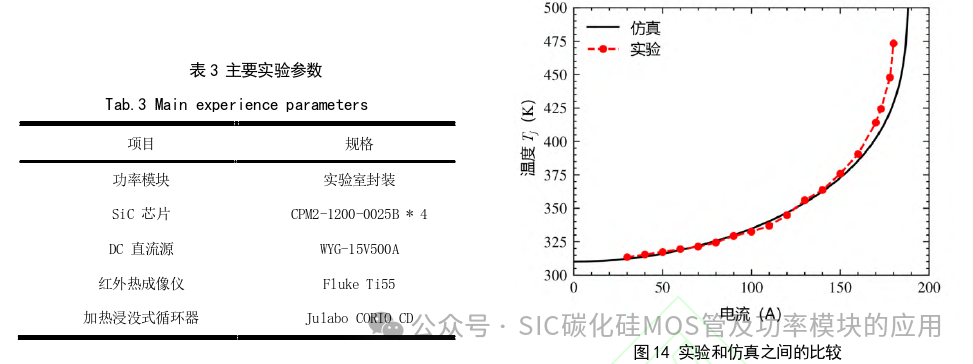 实验过程如下:1)施加恒定电流对Si C器件进行加热,2)等待达到稳定状态,用红外热像仪测量结温,3)记录 漏源电压和电流用于热阻计算。 3.3 结果和讨论 应用前两节的模型,进行电热联合仿真,图14为仿真结果与实验结果的对比。功率模块实测最大导通电流能力为 180A,仿真结果为188 A,结果吻合得比较好,误差约4%。但是,在接近极限运行条件时,在相对较高的电流和温度 下,实测的温度比仿真结果的上升速度要快得多。这是一个突出的现象,它意味着更多的因素可能会影响功率模块在 高温下的热稳定性。本小节将讨论在仿真中没有考虑到的一些因素。
实验过程如下:1)施加恒定电流对Si C器件进行加热,2)等待达到稳定状态,用红外热像仪测量结温,3)记录 漏源电压和电流用于热阻计算。 3.3 结果和讨论 应用前两节的模型,进行电热联合仿真,图14为仿真结果与实验结果的对比。功率模块实测最大导通电流能力为 180A,仿真结果为188 A,结果吻合得比较好,误差约4%。但是,在接近极限运行条件时,在相对较高的电流和温度 下,实测的温度比仿真结果的上升速度要快得多。这是一个突出的现象,它意味着更多的因素可能会影响功率模块在 高温下的热稳定性。本小节将讨论在仿真中没有考虑到的一些因素。 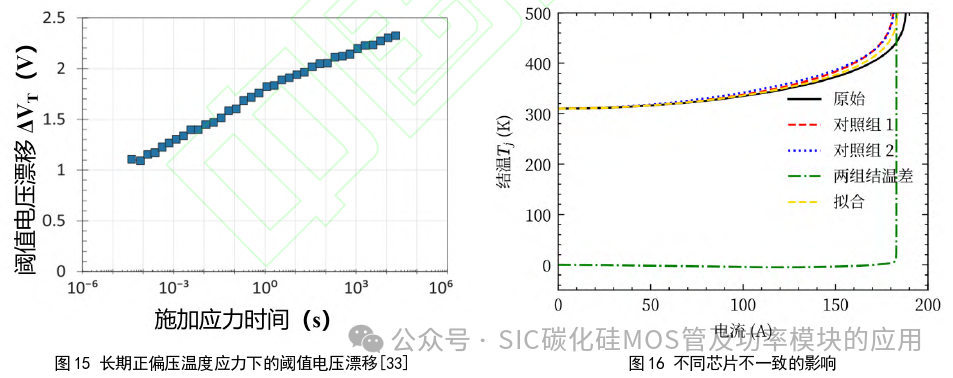 3.3. 1Vth 漂移 阈值电压稳定性主要受绝缘栅氧层近界面区域中的有源电荷陷阱的影响。目前为止,SiC功率MOSFET的SiC/SiO2 界面质量相对较差,其可靠性一直是业界关注的焦点,而它的主要问题是阈值电压的漂移。通常在高温下,阈值电压在正栅极偏压下会有正漂移,在负栅极偏压下会有负漂移;并且栅极偏置时间越长,阈值电压漂移越大,如图 15 所 示。 在本文中,如果在400K时阈值电压增加1V,则通态电阻将增加1mΩ。如果施加160A电流和0.25 K/W热阻, 将发生6.4 K温度升高。 3.3.2 多芯片并联的温度分布 由于并联芯片的个体差异,不同的芯片导通电阻不同,将会导致温度不相等。通常情况下,导通电阻的温度系数为正,当器件温度升高时,其电阻也会增加,这时,通过它的电流减小,温度下降。这种负反馈机制会降低不同的芯片之间温度的不平衡性。但是,在高温下,通态电阻随着温度越来越快地增加,当反馈的速度不能及时缓解温度不平衡时,热失控就会发生。 下面通过仿真来解释这种现象,仍然以本文研究的芯片为例。四个并联的芯片被分为两组,冷却条件相同。第1 组电阻保持原值,第2组增加10%。仿真结果如图16所示,可以发现:当离热失控状态很远时,电阻较大的那一组温度稍高,但两组几乎保持相同的温度;但是接近热失控状态时,电阻较小的组反而具有更高的温度。作为对比,黑色实线使用了图14中的仿真结果,即所有芯片阻值都相同的情况,黄色虚线为所有芯片都相同但是其总阻值与第2组相同时的情况。无论与哪种情况对比,特性不平衡的芯片都会带来更不稳定的高温特性,从而减小模块导通电流的最大导通能力。在本仿真中,不平衡情况下的极限工作电流只有182A。 在未来的分析中考虑这两个非理想因素,所预测出的功率模块的极限电流导通能力将更接近实际值。 4 结论 本文介绍了一种评估功率模块高温下最大电流导通能力的方法。建立了温度相关的SiC MOSFET电气模型和功率模块与散热系统的热模型。对于SiC MOSFET模型,首先研究了与温度相关的物理参数。然后通过实验提取不同温度下的通态电阻。通态电阻分为两部分,Rch和Rs。本文分别对它们两者的温度相关性进行建模,发现Rs随温度呈指数增长, 而Rch随温度有所下降。对于热模型,不是简单地应用恒定热阻,本文通过有限元仿真对热模型的非线性进行了分析。在本文中,热阻被认为几乎与发热功率无关,但对温度较为敏感。 接下来本文阐述了热失控过程的机理,分别讨论了保持热稳定状态和达到热失控状态的条件。最后,结合SiC热电耦合模型和外部散热系统的热模型进行联合仿真,获取了功率模块的最大导通电流的能力。同时设计了实验测试来验证所提出的模型,实验结果与仿真估计误差在4%左右。最后讨论了Vth漂移和多芯片电阻和温度分布不平衡两个非理想因素的影响,估计误差可以进一步降低。
3.3. 1Vth 漂移 阈值电压稳定性主要受绝缘栅氧层近界面区域中的有源电荷陷阱的影响。目前为止,SiC功率MOSFET的SiC/SiO2 界面质量相对较差,其可靠性一直是业界关注的焦点,而它的主要问题是阈值电压的漂移。通常在高温下,阈值电压在正栅极偏压下会有正漂移,在负栅极偏压下会有负漂移;并且栅极偏置时间越长,阈值电压漂移越大,如图 15 所 示。 在本文中,如果在400K时阈值电压增加1V,则通态电阻将增加1mΩ。如果施加160A电流和0.25 K/W热阻, 将发生6.4 K温度升高。 3.3.2 多芯片并联的温度分布 由于并联芯片的个体差异,不同的芯片导通电阻不同,将会导致温度不相等。通常情况下,导通电阻的温度系数为正,当器件温度升高时,其电阻也会增加,这时,通过它的电流减小,温度下降。这种负反馈机制会降低不同的芯片之间温度的不平衡性。但是,在高温下,通态电阻随着温度越来越快地增加,当反馈的速度不能及时缓解温度不平衡时,热失控就会发生。 下面通过仿真来解释这种现象,仍然以本文研究的芯片为例。四个并联的芯片被分为两组,冷却条件相同。第1 组电阻保持原值,第2组增加10%。仿真结果如图16所示,可以发现:当离热失控状态很远时,电阻较大的那一组温度稍高,但两组几乎保持相同的温度;但是接近热失控状态时,电阻较小的组反而具有更高的温度。作为对比,黑色实线使用了图14中的仿真结果,即所有芯片阻值都相同的情况,黄色虚线为所有芯片都相同但是其总阻值与第2组相同时的情况。无论与哪种情况对比,特性不平衡的芯片都会带来更不稳定的高温特性,从而减小模块导通电流的最大导通能力。在本仿真中,不平衡情况下的极限工作电流只有182A。 在未来的分析中考虑这两个非理想因素,所预测出的功率模块的极限电流导通能力将更接近实际值。 4 结论 本文介绍了一种评估功率模块高温下最大电流导通能力的方法。建立了温度相关的SiC MOSFET电气模型和功率模块与散热系统的热模型。对于SiC MOSFET模型,首先研究了与温度相关的物理参数。然后通过实验提取不同温度下的通态电阻。通态电阻分为两部分,Rch和Rs。本文分别对它们两者的温度相关性进行建模,发现Rs随温度呈指数增长, 而Rch随温度有所下降。对于热模型,不是简单地应用恒定热阻,本文通过有限元仿真对热模型的非线性进行了分析。在本文中,热阻被认为几乎与发热功率无关,但对温度较为敏感。 接下来本文阐述了热失控过程的机理,分别讨论了保持热稳定状态和达到热失控状态的条件。最后,结合SiC热电耦合模型和外部散热系统的热模型进行联合仿真,获取了功率模块的最大导通电流的能力。同时设计了实验测试来验证所提出的模型,实验结果与仿真估计误差在4%左右。最后讨论了Vth漂移和多芯片电阻和温度分布不平衡两个非理想因素的影响,估计误差可以进一步降低。 
*博客内容为网友个人发布,仅代表博主个人观点,如有侵权请联系工作人员删除。